Making a virtual machine in Google Sheets
I recently noticed that Google Docs has a pretty full-featured scripting system called Apps Script. It lets you write JavaScript to do some pretty useful things:
- Run code in response to events like documents opening or cells changing
- Make custom Google Sheets spreadsheet functions for formulas
- Use services like Google Translate to translate text or Gmail to send email
- Add new menu items to the Google Docs interface with your custom features
So naturally I had to do something weird with it. Behold: the Google Sheets Virtual Machine generating fibonacci numbers!
How it works
The VM has a memory area of 100 cells, indexed as 0-99. Each cell can contain an instruction or an integer value.
There's also a stack, which starts at the bottom of the memory area and grows upward.
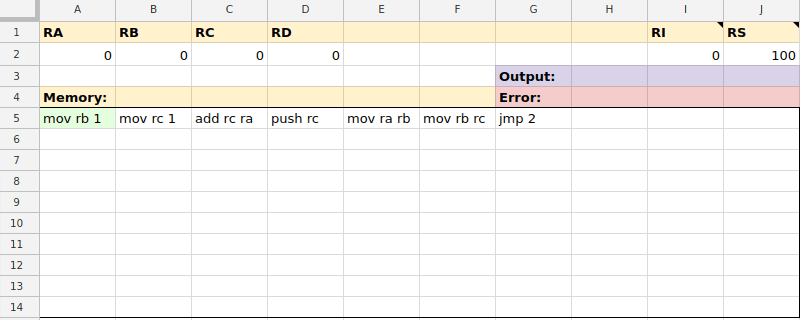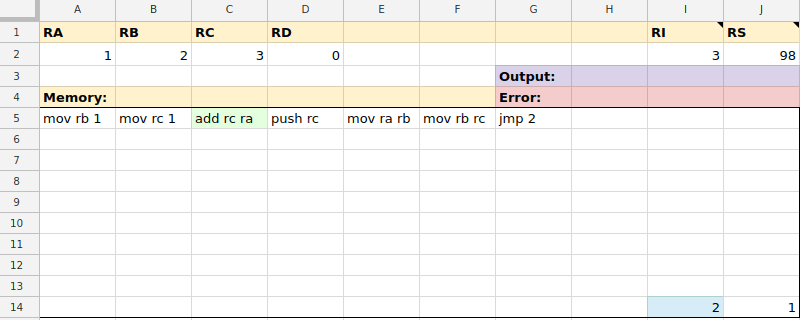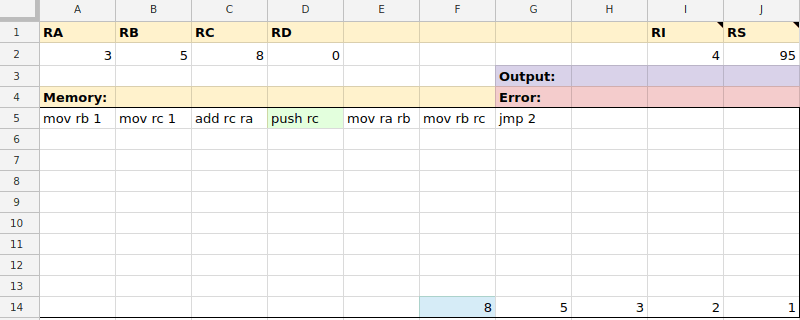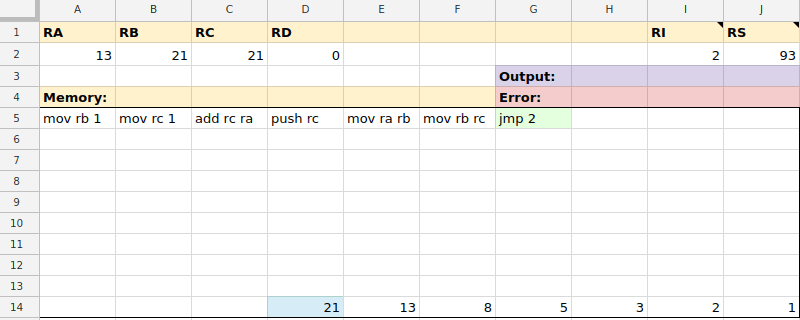
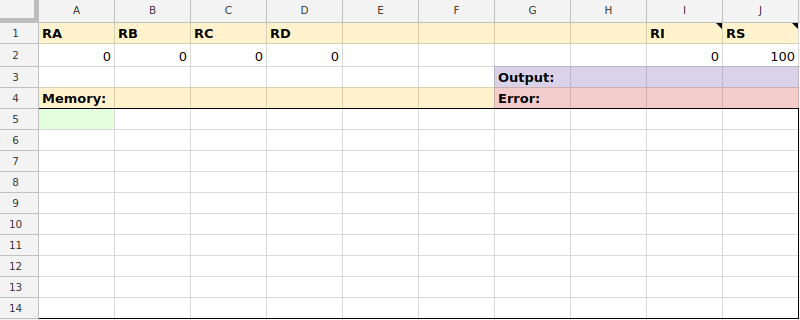
Here's how the VM sheet looks when it's empty:
Notice the following:
- RA, RB, RC, and RD are general purpose registers.
- RI is the instruction pointer. It points to the next instruction to be executed in the memory area, which lights up green.
- RS is the stack pointer. It points to the memory cell at the top of the stack. This lights up blue.
- Output displays the output of a program.
- Error displays any errors encountered in parsing or executing an instruction.
- Memory is a region of 100 cells of memory.
To run an instruction, the Apps Script in the background checks the value of RI to see which instruction to execute next. It reads the instruction in the cell RI is pointing to and parses it.
There are instructions to move data around between memory and registers, manipulate the stack, or perform conditionals.
After the instruction has been executed, the value of RI is incremented to point to the next cell in memory.
Usage
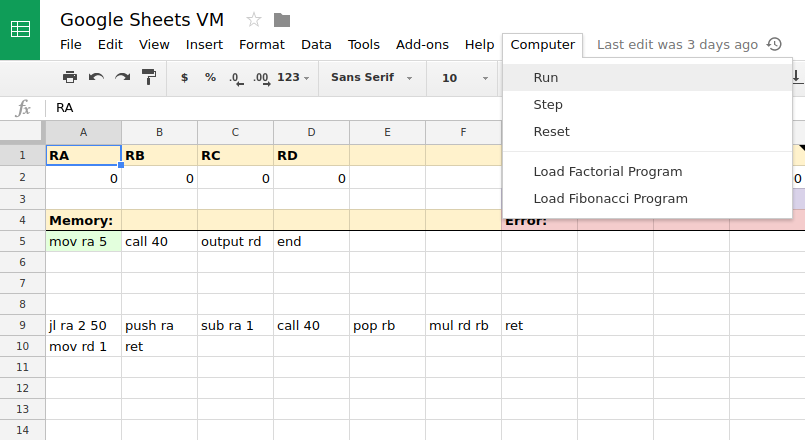
There is a custom menu called Computer with some functions used to control the VM:
- Run will run the current program until it ends or an error is encountered.
- Step runs one instruction and then pauses.
- Reset clears all registers and the output field, which makes the program ready to run again.
- Load Factorial Program loads the factorial example from another sheet.
- Load Fibonacci Program loads the fibonacci example from another sheet.
Instructions
There are a few instructions implemented.
General
- mov dst src copies a value from src to dst.
Math
-
add dst src adds dst to src and stores the result in dst.
-
sub dst src subtracts src from dst and stores the result in dst.
-
mul dst src multiplies dst by src and stores the result in dst.
Stack operations
-
push src pushes src onto the stack.
-
pop dst pops a value off the top of the stack and stores it in dst.
Jumps and conditionals
-
jmp target jumps to the instruction in the cell referenced by target.
-
jl cmp1 cmp2 target compares cmp1 to cmp2. If cmp1 is less than cmp2, execution jumps to target.
Functions
-
call target is a function call. It pushes the current instruction pointer onto the stack so it can be returned to later, and then jumps to target.
-
ret returns from a function. It pops a value off the stack and jumps to it.
Assorted
-
output src writes src to the Output: section of the interface.
-
end ends the program.
Addressing modes
The operands in the instructions above can take a few forms:
Immediates are literal values embedded into the instruction. Examples are:
7 and 123. So to copy the value 7 into the register ra:
mov ra 7
Registers refer to registers by name. Examples are: ra, rb, rc. To
copy the value from rc into rb:
mov rb rc
Memory refers to a value inside a cell of the memory area. Examples are:
$0, $10, $99. To copy the value from ra into the first memory cell:
mov $0 ra
To copy the value from the last memory cell into rd:
mov rd $99
Indirect refers to the value a cell of memory is pointing to. Examples are:
@15, @50. So if memory cell 10 contained the value 20 and memory cell 20
contained the value 30, you could copy the value 30 into ra like this:
mov ra @10
It looks at memory cell 10 to find the value 20. Then it looks at memory cell 20 to find the value 30 and copies that value into ra.
Recursion
You can use the stack and the call and ret instructions to make recursive calls. Here's an example which uses recursion to generate the factorial of the number 5:
The code starting at jl ra 2 50 is a function which takes an input in ra
and returns a result in rd. It calls itself recursively to calculate the
factorial of the value in ra.
Getting a copy
If you want to play around with this yourself, you can make a copy of it here.
You can see the Apps Script code by going to Tools and then Script Editor.